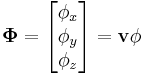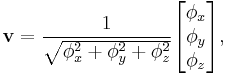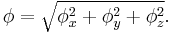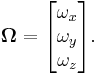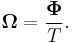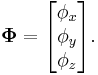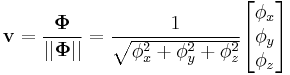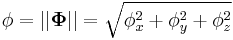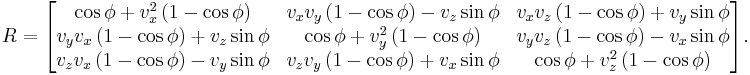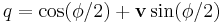Simultaneous orthogonal rotations angle

A simultaneous orthogonal rotations angle (SORA) is a vector representing angular orientation of a rigid-body relative to some reference frame. The components of this vector are equal to the angles of three simultaneous rotations around the rigid body's intrinsic coordinate system axes, initially aligned with the axes of the reference frame, needed to move the rigid body to its current angular orientation. ^[1]^[2]

Every angular orientation can be represented by a single rotation. Therefore, the three simultaneous orthogonal rotations actually represent a single rotation around a certain axis v and for a certain angle $\phi$ . The orientation and magnitude of SORA are equal to this equivalent single rotation axis v and angle $\phi$ , respectively. SORA is therefore the rotation vector, i.e., the vector aligned with the rotation axis and with the length equal to the rotation angle.

1 SORA orientation representation
2 SORA components related to gyroscope measurements
3 Other orientation representations
- 3.1 Conversion from SORA to other orientation representations
4 SORA advantages
5 See also
6 References

SORA orientation representation

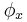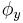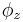Using SORA, angular orientation of a rigid body is indicated with a single rotation equivalent to three simultaneous rotations around the rigid body's intrinsic orthogonal axes initially aligned with the axes of the reference frame. Denoting the angles of the three simultaneous orthogonal rotations with $\phi_x$ , $\phi_y$ , and $\phi_z$ , SORA is equal to:

$\mathbf{\Phi}=\begin{bmatrix} \phi_x \\ \phi_y \\ \phi_z \end{bmatrix}=\mathbf{v}\phi$

where v and $\phi$ are the equivalent single rotation axis and angle respectively, equal to:

$\mathbf{v}=\frac{1}{\sqrt{\phi_x^2%2B\phi_y^2%2B\phi_z^2}}\begin{bmatrix} \phi_x \\ \phi_y \\ \phi_z \end{bmatrix},$

$\phi=\sqrt{\phi_x^2%2B\phi_y^2%2B\phi_z^2}.$

An analytic derivation of these single rotation equivalent axis and angle is achieved by decomposing the total rotation to an infinite sequence of infinitesimally small rotations.^[2]

SORA components related to gyroscope measurements

The most common scenario, where simultaneous rotation around three orthogonal axes can be observed is when performing measurements with a gyroscope. By providing angular velocity measurements, gyroscopes can also be used in angular orientation estimation. Here, the gyroscope itself is considered the rigid body and inertial space the reference system; the measured angular velocities indicate the rotation needed to move the gyroscope to its current angular orientation. To fully specify angular orientation in inertial space, the gyroscope must be suitable for measuring angular velocities around all three intrinsic coordinate system axes (i.e., it must be a 3D gyroscope). Because rotations in general are not commutative, one cannot treat the three simultaneous angular velocities measured with a 3D gyroscope as sequential rotations. There are six possible sequences of three orthogonal rotations and, thus, six different angular orientations. None of these yields the correct angular orientation for simultaneous rotations.

The three simultaneous orthogonal rotations measured with a 3D gyroscope represent a single rotation around a certain axis for a certain angle. When the measured angular velocities or their proportions are constant, this rotation and the resulting angular orientation can be uniquely represented with SORA. When this condition is met, the orientation of the rotation axis does not change and the components of SORA are equal to the angles of three simultaneous rotations measured with a 3D gyroscope.

Using gyroscope measurements that provide rotation angle estimation, it is reasonable to combine angular velocities around three orthogonal axes in vector form:

$\mathbf{\Omega}=\begin{bmatrix} \omega_x \\ \omega_y \\ \omega_z \end{bmatrix}.$

Angular velocity vector $\Omega$ is orthogonal to the rotation plane, and its magnitude is equal to the angular velocity in that plane. When the measured angular velocities or their proportions are approximately constant, the orientation of the rotation axis is also constant. It then holds:

$\mathbf{\Omega}=\frac{\mathbf{\Phi}}{T}.$

Other orientation representations

Different representations for rigid body angular orientation exist including Euler angles, rotation matrix, and quaternions. Euler angles represent orientation indicating three sequential rotations. Without considering the possibilities of different signs for the angles or rotating the reference frame, there are twelve different conventions. Moreover, using Euler angles leads to the Gimbal-lock problem, where one degree of freedom is lost. Euler angles provide a means for giving a numerical description of any rotation in three dimensional space using three numbers, but not only is this description not unique, but there are some points where not every change in the target space (rotations) can be realized by a change in the source space (Euler angles).

Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of Gimbal lock. A general quaternion represents a point in a four dimensional space, but constraining it to have unit magnitude yields a three dimensional space equivalent to the surface of a hypersphere. The vector part of a unit quaternion represents the radius of the 2-sphere corresponding to the axis of rotation, and its magnitude is the cosine of half the angle of rotation.

Angular orientation can also be represented with a rotation matrix. Any rotation in three dimensions can be described by a rotation around a certain axis and for a certain angle. The angle and axis are implicitly represented by the entries of the rotation matrix. If rotation matrices are used to represent Euler rotations, the Gimbal lock problem again occurs.

Conversion from SORA to other orientation representations

Let us again use the following denotation for SORA:

$\mathbf{\Phi}=\begin{bmatrix} \phi_x \\ \phi_y \\ \phi_z \end{bmatrix}.$

The orientation and magnitude of SORA are equal to the rotation axis v and angle $\phi$ , respectively:

$\mathbf{v}=\frac{\mathbf{\Phi}}{||\mathbf{\Phi}||}=\frac{1}{\sqrt{\phi_x^2%2B\phi_y^2%2B\phi_z^2}}\begin{bmatrix} \phi_x \\ \phi_y \\ \phi_z \end{bmatrix}$

and

$\phi=||\mathbf{\Phi}||=\sqrt{\phi_x^2%2B\phi_y^2%2B\phi_z^2}$

To obtain the entries of a rotation matrix R or components of a quaternion q, indicating the same rotation, we simply insert the above axis and angle in the appropriate rotation matrix and quaternion expressions:

$R = \begin{bmatrix} \cos \phi %2Bv_x^2 \left(1-\cos \phi\right) & v_x v_y \left(1-\cos \phi\right) - v_z \sin \phi & v_x v_z \left(1-\cos \phi\right) %2B v_y \sin \phi\\ v_y v_x \left(1-\cos \phi\right) %2B v_z \sin \phi& \cos \phi%2B v_y^2\left(1-\cos \phi\right) & v_y v_z \left(1-\cos \phi\right) - v_x \sin \phi\\ v_z v_x \left(1-\cos \phi\right) - v_y \sin \phi& v_z v_y \left(1-\cos \phi\right) %2B v_x \sin \phi& \cos \phi%2B v_z^2\left(1-\cos \phi\right) \end{bmatrix}.$

$q = \cos (\phi/2) %2B \mathbf{v} \sin (\phi/2)$

where R is the rotation matrix indicating a rotation around a single axis coinciding with the vector v = (v_x, v_y, v_z) and for an angle $\phi$ and q is the unit quaternion indicating the same rotation.

SORA advantages

SORA represents a unique angular orientation of a rigid-body relative to some reference frame. Using SORA as a generalized representation of angular orientation, we can avoid the problem of different rotation sequence conventions as in Euler angles. As SORA indicates a single rotation for a specific angular orientation, the Gimbal problem is here avoided.

SORA is simple and well-suited for use in the real-time calculation of orientation based on angular velocity measurements derived using a gyroscope, as long as the measured angular velocities or their proportions are approximately constant. Under this condition, using SORA, orientation calculation only requires a single step. ^[1] SORA is appropriate for use in a number of applications that require angular orientation information, including navigation and motion tracking.

Finally, SORA helps interpret the meaning of the rotation vector with measurable quantities.

References

^ ^a ^b Tomažič, Sašo (2011). "Simultaneous Orthogonal Rotations Angle". Elektrotehniški vestnik - Journal of Electrical Engineering and Computer Science. ISSN 2232-3228. http://ev.fe.uni-lj.si/1-2-2011/Tomazic.pdf.
^ ^a ^b Stančin, Sara (2011). "Angle Estimation of Simultaneous Orthogonal Rotations from 3D Gyroscope Measurements". Sensors. doi:10.3390/s110908536. http://www.mdpi.com/1424-8220/11/9/8536/.